Matemática - Conjuntos Numéricos

Conjuntos Numéricos

• Números naturais (N): Todo número inteiro positivo, incluindo o zero. Pode ser representado da seguinte maneira:

       N = {0,1,2,3,4,5,6...}

      É um conjunto infinito.

• Números inteiros (Z): Todo número positivo ou negativo, não decimal. Pode ser representado da seguinte maneira:

       Z = {...-4,-3,-2,-1,0,1,2,3,4...}

• Números Racionais (Q): Todo número que pode ser escrito na forma de fração. Pode ser representado da seguinte maneira:

       
   
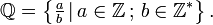
        Subconjuntos de Q :
  ---------------------------------- é o conjunto dos números racionais não nulos (diferentes de zero).

  -------------------------------- é o conjunto dos números racionais positivos e o zero.

  ------------------------------ é o conjunto dos números racionais negativos e o zero.

  ------------------------------ é o conjunto dos números racionais positivos e não nulos.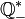

 ----------------------------- é o conjunto dos números racionais negativos e não nulos.

• Números Irracionais (I): Todo número que não pode ser representado por meio de uma fração.

 Ex.: π = 3,14159265...

        φ = 1,61803398...

        l =  2,7182818...

        

OBS.: Números em forma decimal, infinitos e não periódicos.

    

• Números Reais (R): Todo número não complexo.
• Números Complexos (C): Números que possam ser somados e multiplicados, e também possibilitem a extração da raiz quadrada de um número negativo. 

     Forma algébrica:

            z = a+b.i

 Onde: a é a parte real de z  ( Re(z)=a )

            b.i é a parte imaginária de z ( Im(z) = b.i )      

          i é a unidade imaginária, tal que i²=-1.